Diffie-Hellman-Härteannahme:
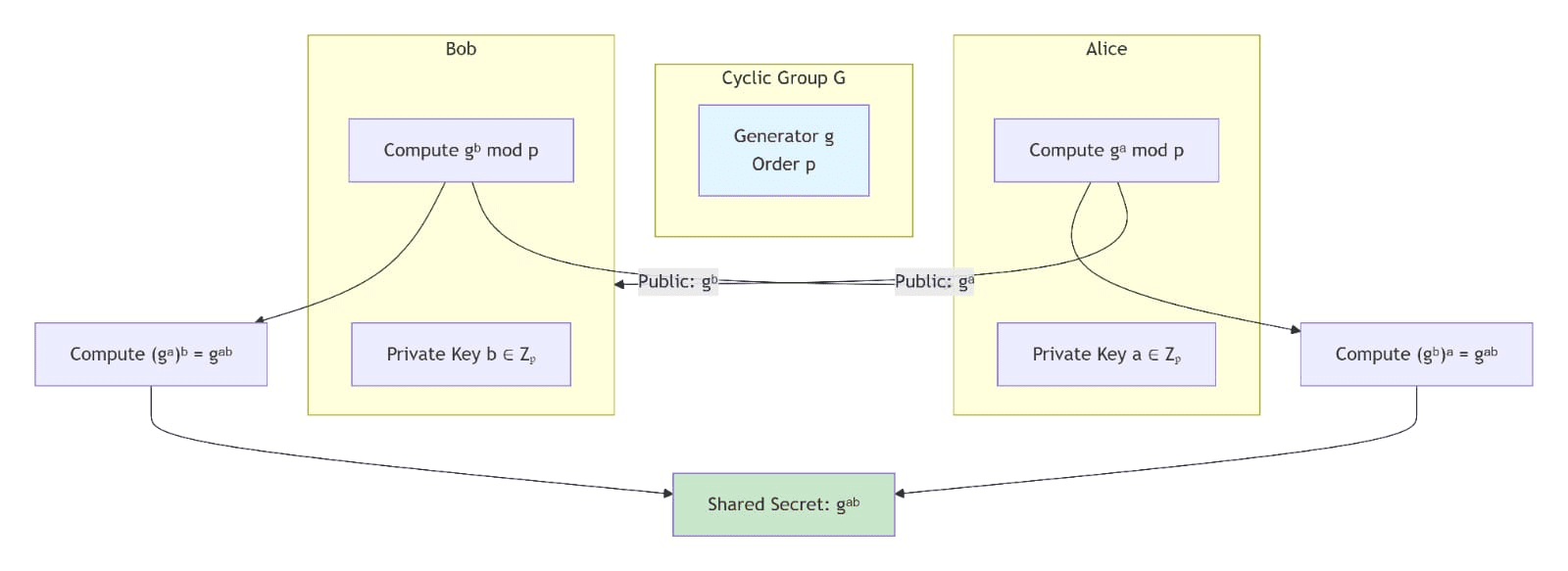
In jeder Gruppe ist ein diskreter Logarithmus loдb a eine Zahl x ∈ Z, sodass bx = a gilt.
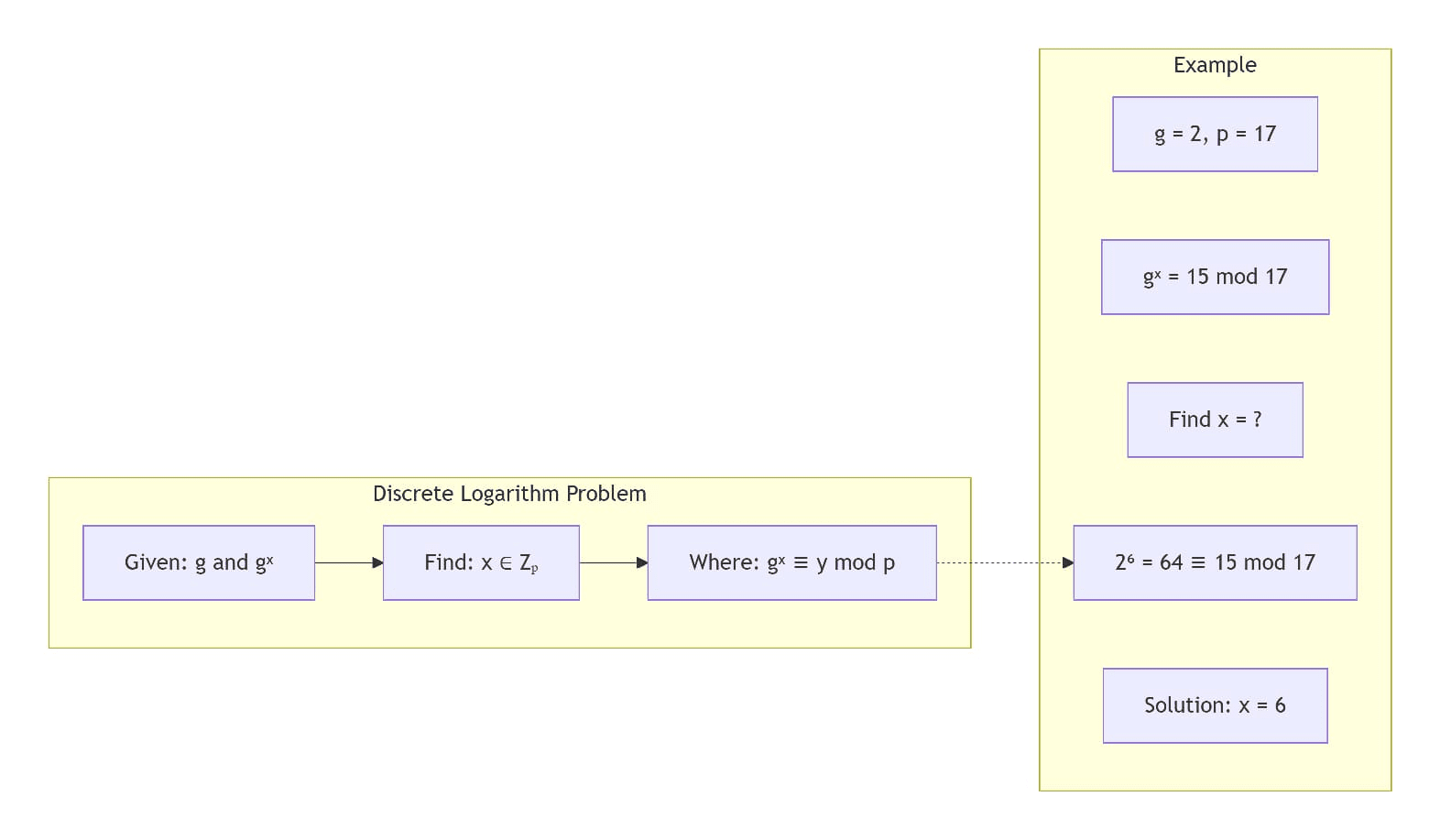
Die meisten kryptographischen Bausteine, die mit dieser Arbeit zusammenhängen, sind mit der Diffie-Hellman-Annahme verbunden, die die Schwierigkeit des diskreten Logarithmus in zyklischen Gruppen nutzt.
Betrachtet man eine multiplikative zyklische Gruppe G der Ordnung p und einen Erzeuger д, so
kann die folgende Annahme formulieren: Gegeben дa und дb für gleichmäßig und unabhängig gewählte a, b ∈ Zp, verhält sich дab wie ein zufälliges Element in G mit der Ordnung p.
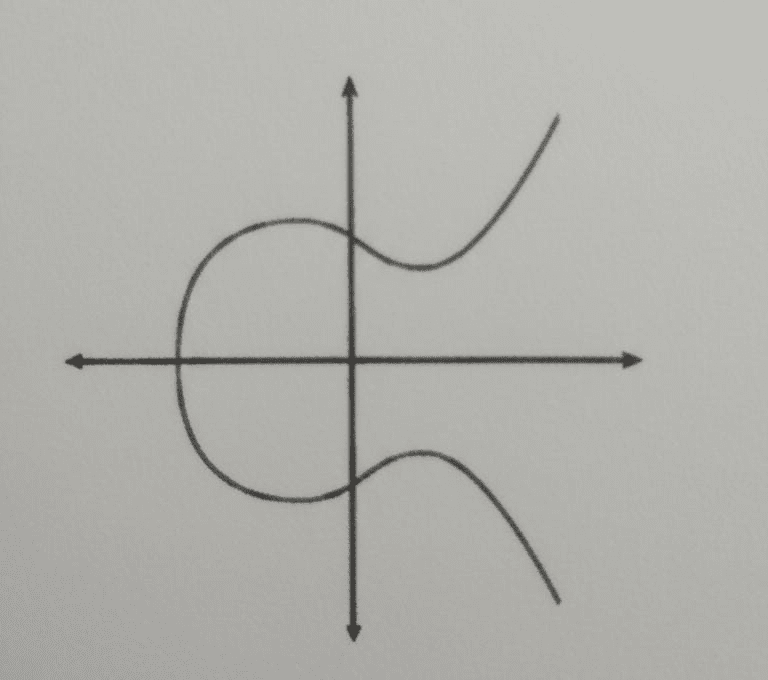
In der obigen Abbildung ist A eine generische elliptische Kurve.
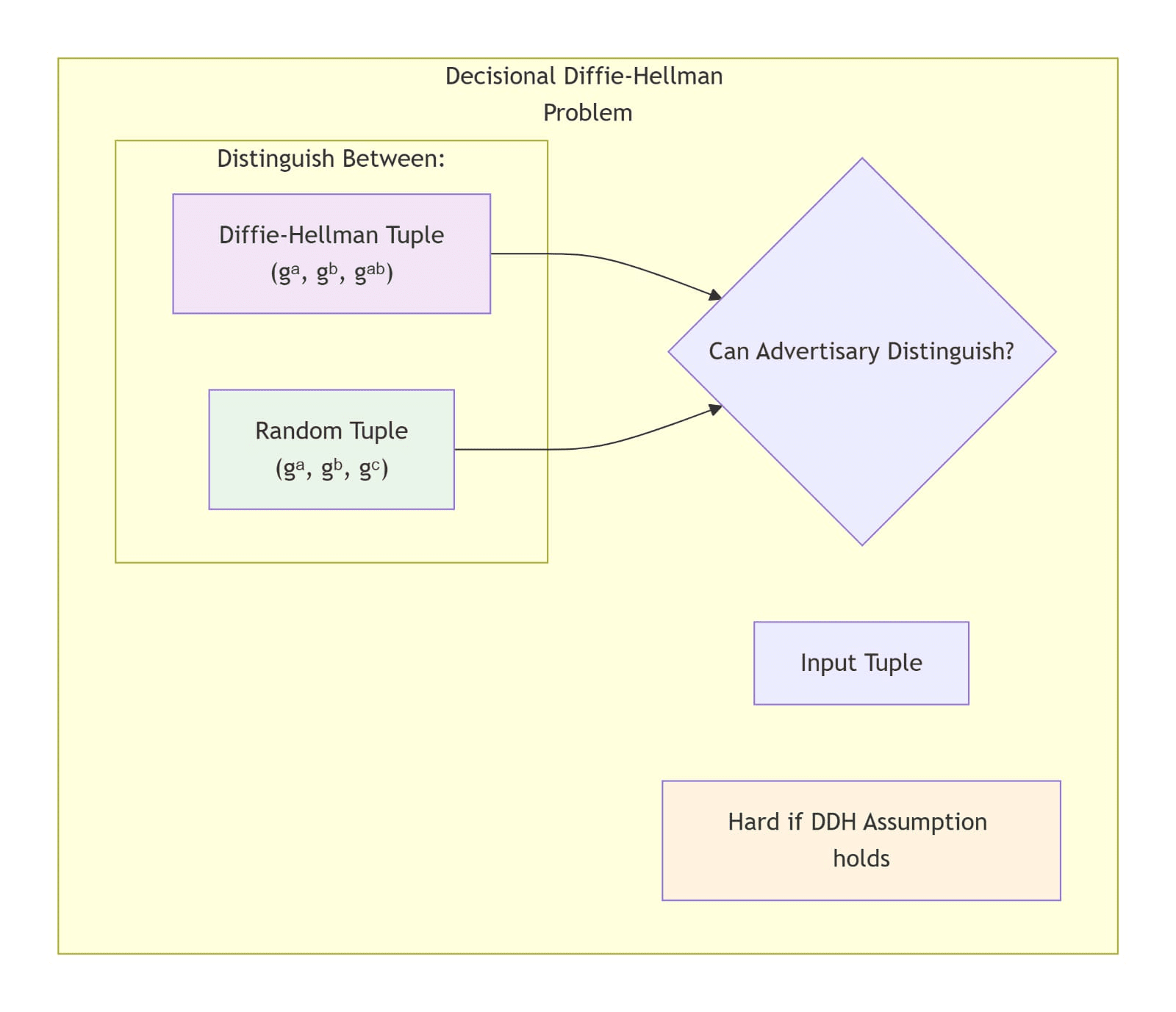
Als Folge solcher angenommenen Zufälligkeit bezieht sich das Entscheidungs-Diffie-Hellman (DDH)-Problem auf die Unterscheidung der folgenden beiden Wahrscheinlichkeitsverteilungen:
• (дa ,дb ,дab ) ∀a,b ∈ Z
// (дa ,дb ,дab ) sind als Diffie-Hellman-Tuple definiert
• (дa ,дb ,дc) ∀a,b,c ∈ Z
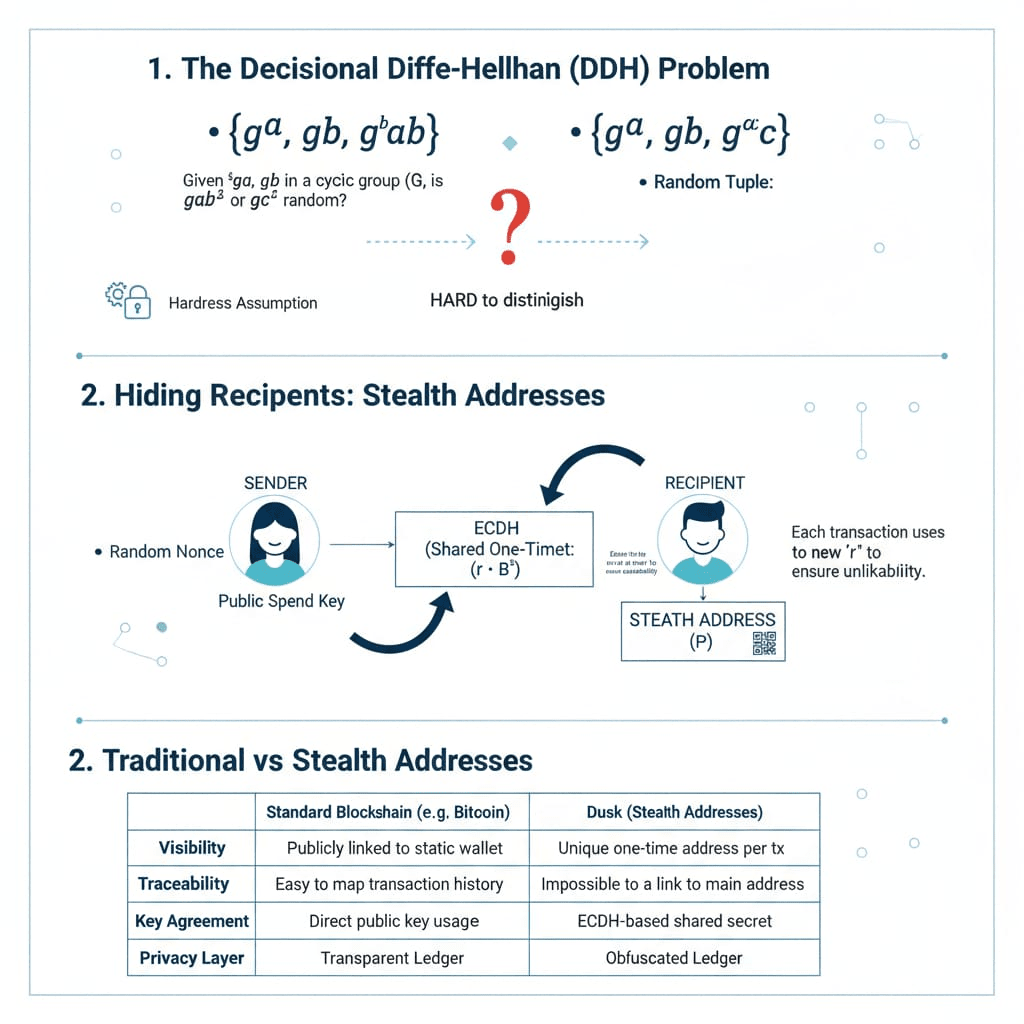
• Versteckte Empfänger: Stealth-Adressen
Inspiriert von dem CryptoNote-Whitepaper basiert die Technologie der Stealth-Adressen auf der #Dusk -Technik zum Verstecken von Empfängern. Sie wurde bereits umfassend in anderen datenschutzorientierten digitalen Währungen getestet und ist die bewährte Wahl, um die wahre Empfängeradresse einer Transaktion zu verbergen, während die Einzigartigkeit im Kontext des Ledgers gewahrt bleibt (was bedeutet, dass keine andere Adresse mit einer Stealth-Adresse verknüpft werden kann). Darüber hinaus ist eine Ableitung einer unbegrenzten Anzahl von Empfangsadressen ebenfalls möglich, ohne dass eine von ihnen eine Rückverfolgbarkeit zur Hauptadresse des Empfängers erlaubt. Als anonymes Schlüsselvereinbarungsprotokoll verwendet Dusk das elliptische Kurven-Diffie-Hellman (ECDH) aufgrund der gewünschten Eigenschaft, dass zwei Parteien ein gemeinsames Geheimnis generieren können, indem sie lediglich den öffentlichen Schlüssel des anderen und den Generatorpunkt der in der Twisted-Edward-Gleichung verwendeten elliptischen Kurve kennen.
• Kryptografische Bausteine:
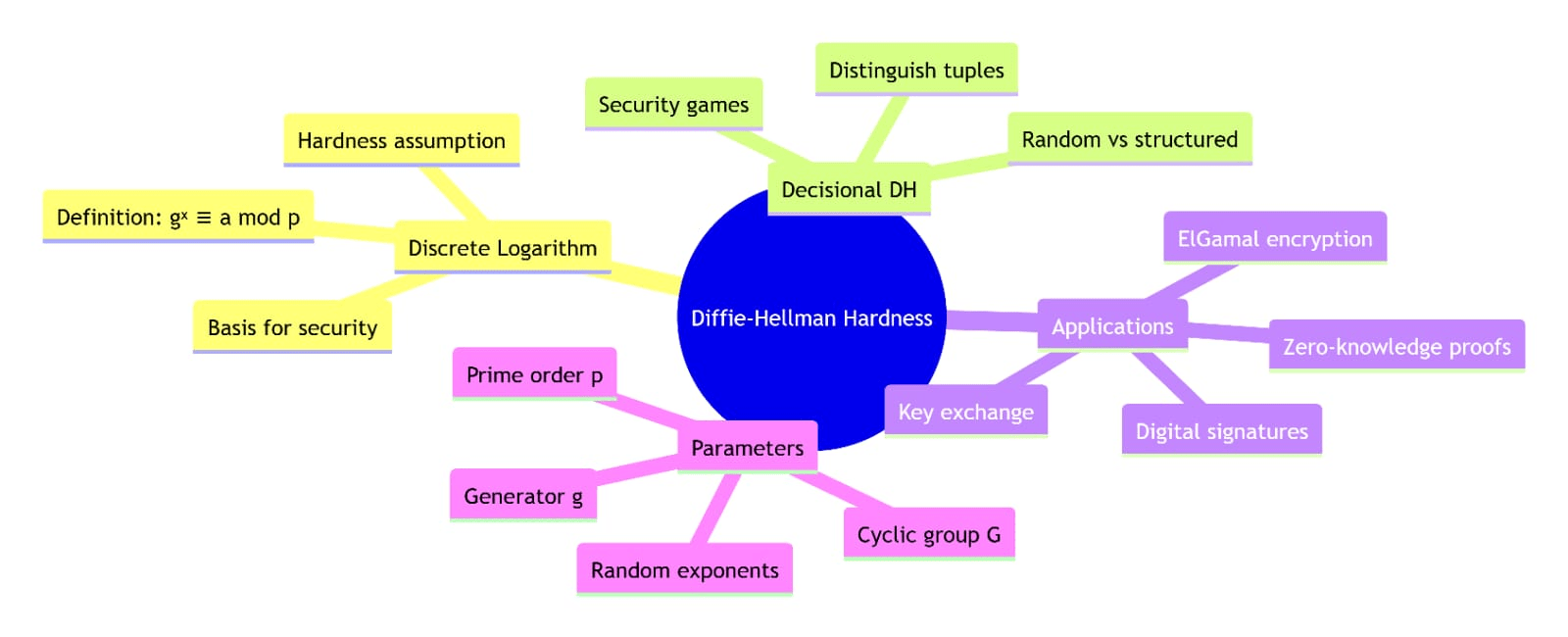
Diese Diagramme visualisieren:
Der Diffie-Hellman-Schlüsselaustauschprozess
Definition des diskreten Logarithmusproblems
DDH-Unterscheidungsherausforderung
Gruppenstruktur und Eigenschaften
Mathematische Beziehungen zwischen Annahmen
Sicherheitsnachweis-Reduktionen
DH-Tuple vs. zufälliger Tuple-Vergleich
Verteilung der Gruppenelemente
Diese zeigen die mathematischen Konzepte, die in der Vorarbeit von @Dusk verwendet werden.
