Diffie-Hellman Hardness Assumption:
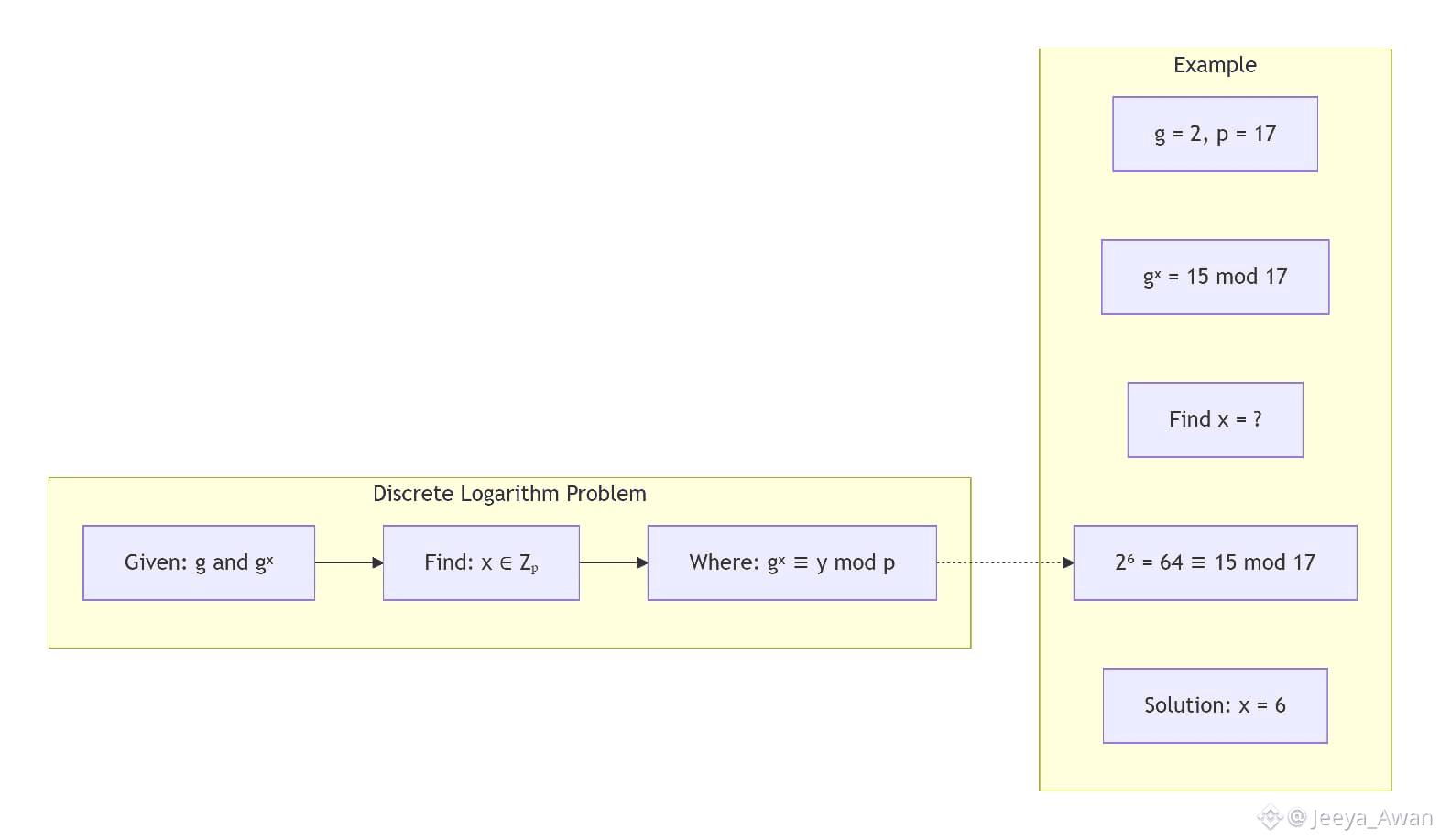
In any group, a discrete logarithm loдb a is a number x ∈ Z such that bx = a.
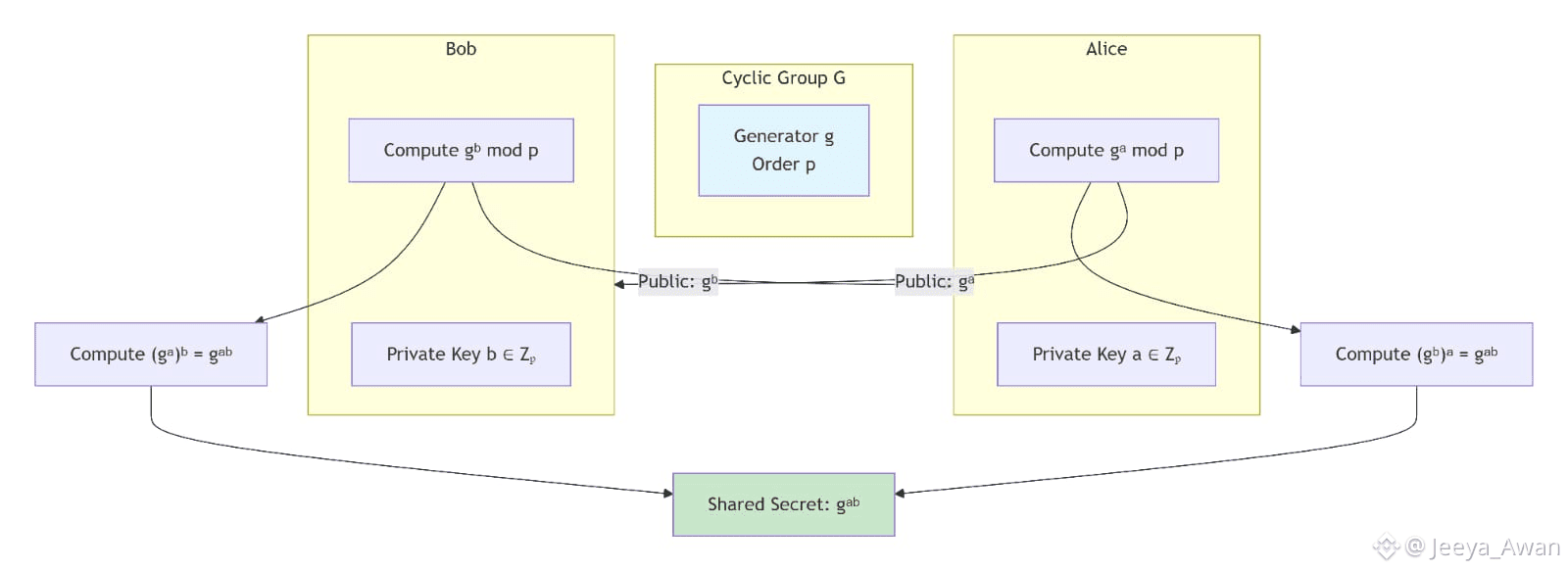
Most of the cryptographic building blocks related to this work are linked to the Diffie-Hellman assumption which uses the hardness of discrete logarithms in cyclic groups .
Considering a multiplicative cyclic group G of order p and generator д, we
can formulate the following assumption: given дa and дb for uniformly and independently chosen a ,b ∈ Zp then дab performs like a random element in G of order p.
In above figure is A generic elliptical curve.
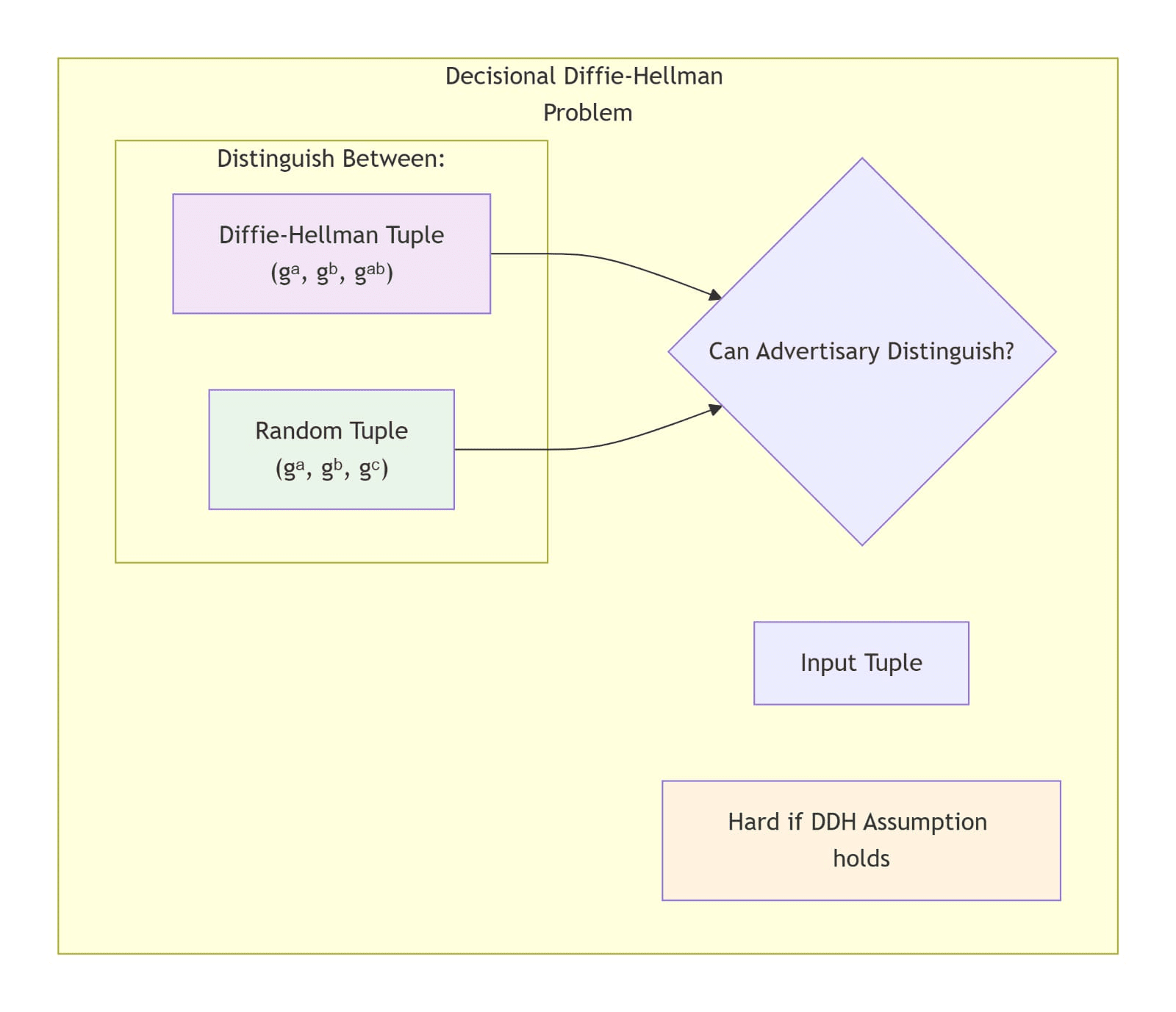
As a consequence of such assumed randomness, the Decisional Diffie-Hellman (DDH) Problem relates to distinguishing the following two probability distributions:
• (дa ,дb ,дab ) ∀a,b ∈ Z
// (дa ,дb ,дab ) are defined as a Diffie-Hellman Tuple
• (дa ,дb ,дc) ∀a,b,c ∈ Z
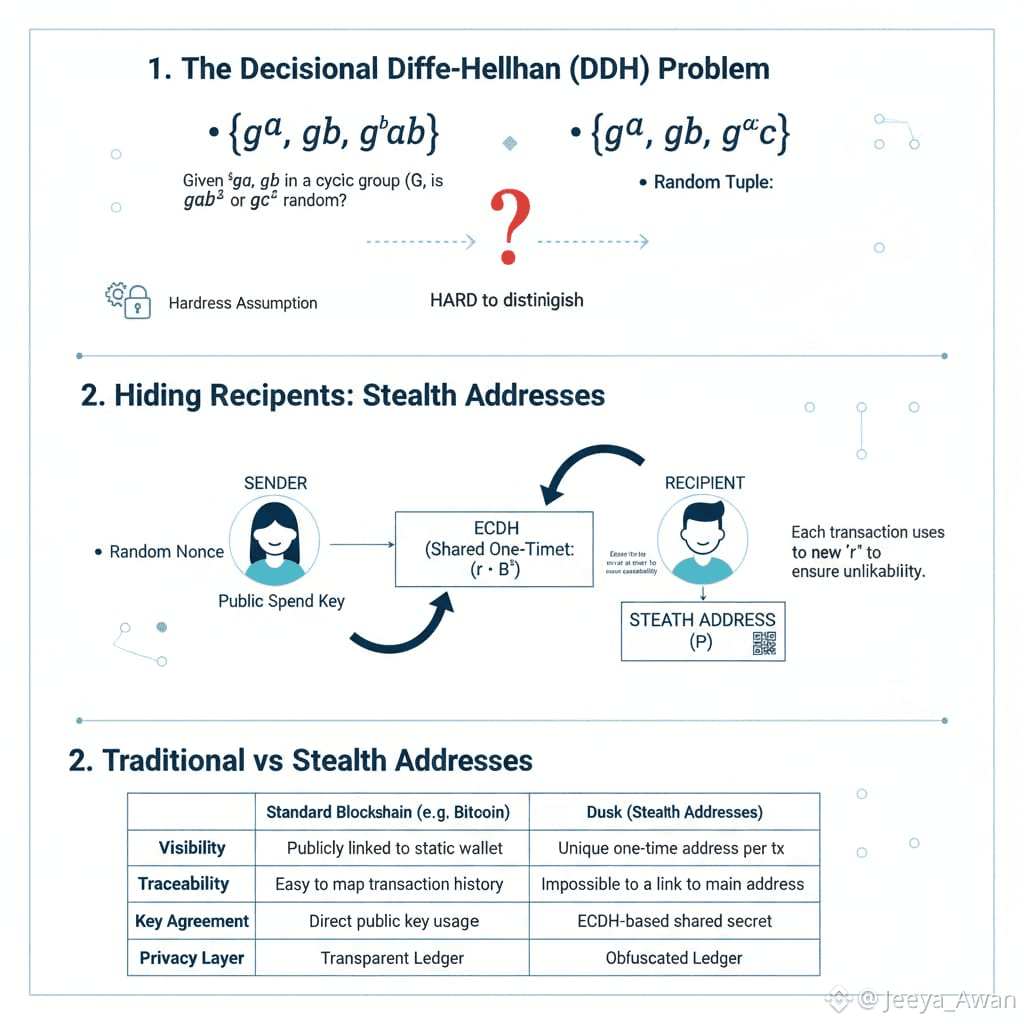
• Hiding Recipients: Stealth Addresses
Inspired by the CryptoNote white-paper, stealth address technology is at the basis of #Dusk recipient hiding technique. Already widely tested in other privacy-oriented digital currencies, it is the proven choice for concealing the true recipient address of a transaction while keeping uniqueness within the context of the ledger (meaning no other address can be linked to a stealth address). Additionally, a derivation of an unbound number of receiving addresses is also possible without any of them allowing traceability back to the recipient’s main address. As an anonymous key agreement protocol, Dusk uses the Elliptic Curve Diffie-Hellman (ECDH) due to the desired property of allowing two parties to generate a shared secret by solely knowing each other’s public key, and the generator point of the Elliptic Curve used in the Twisted Edward equation.
• Cryptographic building blocks:
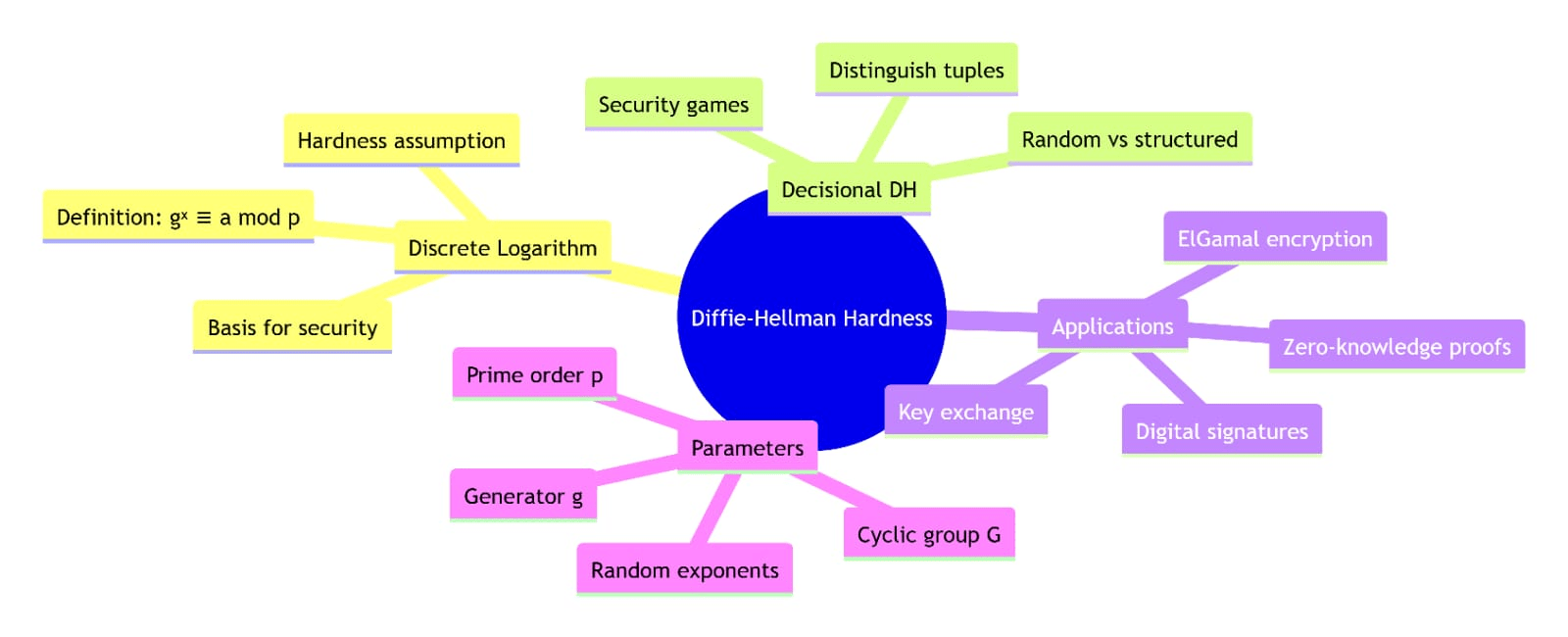
This diagrams visualize:
The Diffie-Hellman key exchange process
Discrete logarithm problem definition
DDH distinguishing challenge
Group structure and properties
Mathematical relationships between assumptions
Security proof reductions
DH tuple vs random tuple comparison
Distribution of group elements
These show the mathematical concepts used in preliminary of @Dusk .
