2. Règles de dérivation [BIP32]
Nous avons généré la seed via BIP39, que nous appelons "seed principale", selon les règles de dérivation BIP32, nous pouvons dériver la "clé privée principale", la "clé publique principale", et la "clé publique principale", ces trois étant appelées "clés". Nous pouvons continuer à utiliser ces "clés" comme "seed fils" pour dériver les "clés fils" ("clé privée fils", "clé publique fils", "clé publique fils"), et ainsi de suite, produisant indéfiniment des descendants, tous dérivés de la "seed principale", donc la "seed principale" est également appelée "racine". La "clé privée principale", la "clé publique principale", et la "clé publique principale" sont également appelées "clés principales". Tant que nous avons sauvegardé les "mots de passe", nous pouvons exporter la "racine" -> "racine principale" -> "racine fils" etc.
Il est clair que chaque niveau de "clé" peut être utilisé à la fois comme "clé privée" et "clé publique" à utiliser directement, ou simplement comme racine pour dériver la "clé" suivante, la manière de les organiser dépendra du protocole "BIP44". En d'autres termes, le BIP32 définit la méthode de préparation, le BIP44 définit si le plat préparé sert d'ingrédient pour le plat suivant ou s'il est consommé directement.
1) Dériver la "clé principale"
Utilisez la chaîne fixe "Bitcoin seed" comme clé "Key", et "seed" comme donnée "Data" entrée dans la fonction HMAC-SHA512(Key, Data) pour générer un nombre binaire de 512 bits, en prenant les 256 premiers bits pour générer la "clé privée principale", et les 256 derniers pour la "clé publique principale". Selon la "clé privée principale", générez la "clé publique principale" selon la méthode de génération de clé publique mentionnée précédemment.
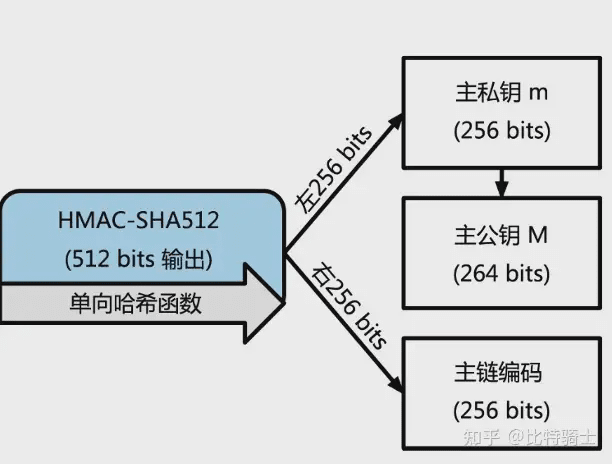
Figure 1, dérivation de la "clé principale" à partir de la "seed"
2) Dériver la "clé fils"
On utilise toujours la fonction HMAC-SHA512(Key, Data) pour dériver les clés fils, mais les paramètres d'entrée de la fonction peuvent utiliser soit la "clé privée principale", soit la "clé publique principale", ce qui fait la différence. Car en utilisant la "clé privée principale", il n'est pas possible de générer la "clé publique fils" via la "dérivation ordinaire", donc nous appelons le mode de dérivation utilisant la "clé privée principale" comme "dérivation par durcissement" et celui utilisant la "clé publique principale" comme "dérivation ordinaire".
Introduire une constante d'index index, et lorsque index ≥ 2^31, utiliser la dérivation par durcissement, sinon utiliser la dérivation ordinaire. Dans les règles BIP32, cela est expliqué avec les deux pseudo-fonctions suivantes.
CKDpriv(clé privée père, clé publique père, index)
CKDpub(clé publique père, clé publique père, index)
Ces deux pseudo-fonctions réalisent la dérivation via la fonction HMAC-SHA512(Key, Data).
Def CKDpriv(k_par, c_par, i):
if I >= 2³¹
data = 0x00 || ser256(k_par) || ser32(i) # Utilisé pour la dérivation par durcissement
sinon
K_par = point(k_par)
data = serP(K_par) || ser32(i) # Utilisé pour la dérivation ordinaire
I = HMAC_SHA512(key = c_par, msg = data) I_L, I_R = I[:32], I[32:]
// Prendre les 256 bits de gauche pour générer la clé privée fils, les 256 bits de droite pour la clé publique fils
k_i = (I_L + k_par) mod n # Mécanisme clé c_i = I_R return k_i, c_i
// Les entrées sont la "clé privée père" et la "clé publique", et les sorties sont la "clé privée fils" et la "clé publique fils"
--------------------------------------------------------------
Def CKDpub((K_par, c_par), i):
if i >= 2³¹ // La dérivation par durcissement ne peut pas être utilisée pour CKDpub
throw InvalidChildError
data = serP(K_par)||ser32(i)
I = HMAC-SHA512(Key = c_par, Data = data)
IL, IR = I[0:32], I[32:64]
K_i = point(IL) + K_par // addition de points sur la courbe elliptique, mécanisme clé
c_i = IR return (K_i, c_i)
// Les entrées sont la "clé publique père" et la "clé publique", et les sorties sont la "clé publique fils" et la "clé publique fils"
Les deux fonctions ci-dessus ont pour fonction :
Lors de la dérivation par durcissement :
La "clé privée fils" dérivée dépend de la "clé privée père", et ne peut pas être générée par "dérivation ordinaire", la sécurité est plus élevée
Lors de la dérivation ordinaire :
Grâce à la "clé privée père" et à la "clé publique père", on peut obtenir la "clé privée fils" et la "clé publique fils" (ici, la "clé privée fils" et la "clé privée fils dérivée par durcissement" sont différentes)
Avec la "clé publique père" et la "clé publique père", on peut seulement obtenir la "clé publique fils"
Cela permet de publier la "clé publique père" et la "clé publique père", de générer un portefeuille d'observation, car sans la clé privée père, il est impossible de générer la clé privée fils, et donc d'opérer le compte

Figure 2, la différence entre les deux fonctions de dérivation lors de la dérivation ordinaire
La fonction de la "clé publique" est d'assurer que deux fonctions génèrent la même "clé publique fils", et de soutenir la génération de l'"arbre de clés"
Voici une nouvelle explication séparée, résumant les deux logiques de dérivation
(1) Dérivation par durcissement
Entrée : clé privée père (k_par), clé publique père (c_par), index (i ≥ 2^31)
Processus :
Calculer I = HMAC-SHA512(c_par, k_par || index)
I_L (256 premiers bits), utilisé pour calculer la clé privée fils
Clé privée fils, k_i = (k_par + I_L) mod n (n étant l'ordre de la courbe elliptique)
I_R (256 derniers bits) : clé publique fils (c_i)
Sortie : clé privée fils (k_i), clé publique fils (c_i)
Caractéristiques : nécessite la clé privée père, ne peut pas être dérivée à partir de la clé publique père, sécurité élevée
(2) Dérivation ordinaire
Entrée : clé publique père (K_par), clé publique père (c_par), index (i < 2^31)
Processus :
Calculer I = HMAC-SHA512(c_par, K_par || index)
I_L : clé privée fils, k_i = k_par + I_L (mod n)
I_R : clé publique fils (c_i)
Clé publique : K_i = point(k_i) (produit de point, courbe secp256k1)
Sortie : clé publique fils (K_i), clé publique fils (c_i).
Caractéristiques : peut être dérivée à partir de la clé publique père, convient pour établir un portefeuille d'observation
(3) Arbre de clés
La clé principale est la racine principale, les clés fils sont dérivées par index niveau par niveau, formant une structure arborescente
Plage d'index : 0 à 2^32-1 (0x00000000 à 0xFFFFFFFF)
Index durci : 2^31 à 2^32-1 (0x80000000 à 0xFFFFFFFF)
Index non durci : 0 à 2^31-1 (0x00000000 à 0x7FFFFFFF)