
« Doms? Unde mergem, nu avem nevoie de doms. »
Pe piețele clasice, avem un Depth of Market (DOM) pentru a vedea adâncimea carnetului de ordine: unde sunt marii cumpărători, unde se ascund vânzătorii, până unde va împinge o ordine prețul.
Dar pe piața Alpha… nu există DOM. 🥶
Cum să plasezi ordinele în progresie geometrică, să gestionezi riscul, să simți dacă piața este adâncă sau superficială când nu vezi carnetul? 🤔
Vom reconstrui o adâncime implicită pe baza mișcării prețului între benzile Bollinger, cu o mică energie discretă (grafic / Laplacian). 💪
1. De ce DOM este atât de valoros (și ce pierdem fără el)
Pe o pereche Spot clasică (BTCUSDT, ETHUSDT…), DOM-ul îți oferă:
cele mai bune oferte și cereri,
volum la fiecare nivel de preț,
profundimea cumulată până la ±0,1 %, ±0,5 %, ±1 %, etc.
Pentru un trader, asta ajută la:
identifică zidurile (blocuri mari de ordine limită),
distribuie un ladder de ordine (progresie geometrică de dimensiuni/prețuri),
să știi dacă un ordin mare va muta prețul cu 0,05 % sau cu 2 %.
Pe piața Alpha, toate acestea sunt invizibile.😱
Nu vezi decât urmele tranzacțiilor în preț.🤷♂️
Ideea: folosește aceste urme pentru a ghici profunzimea ascunsă.💪
2. Pune prețul într-un tunel Bollinger
Pleacă de la o serie de prețuri, la intervale de timp regulate (de exemplu, la fiecare secundă sau la fiecare minut).
2.1. Medie și deviație standard mobile
Pe o fereastră de lungime (de exemplu 20 sau 60 de puncte), se definește:
Formule (1) : medie mobilă
m_L(i) = (1 / N_L) × sumă pentru k de 0 la N_L − 1 de P_{i − k}
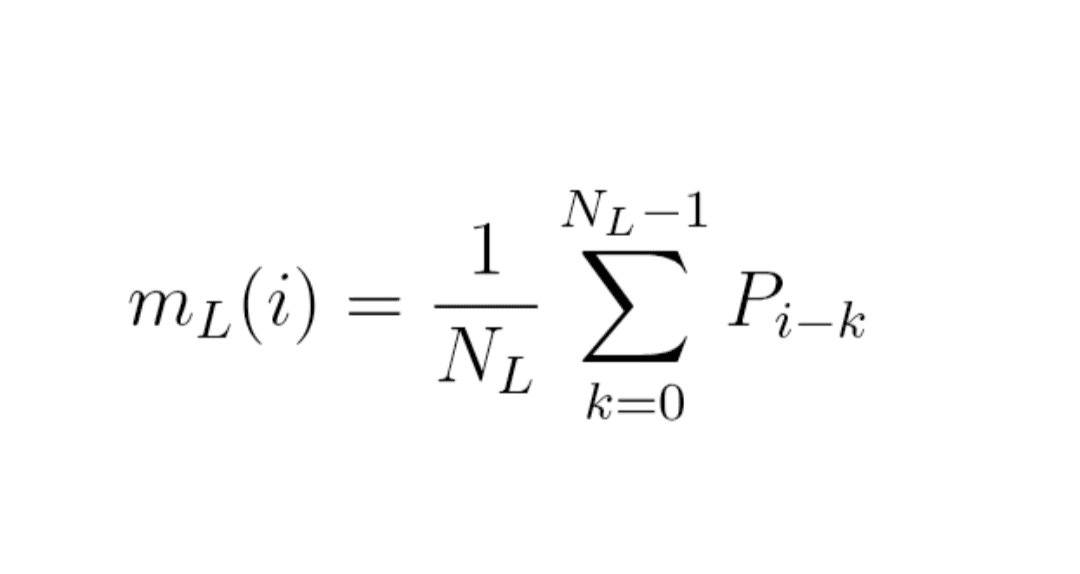
Cu alte cuvinte,
m_L(i) = (P_i + P_{i−1} + … + P_{i−N_L+1}) / N_L.
Formulă (2) : deviație standard mobilă
σ_L(i) = rădăcină pătrată de
[ 1 / (N_L − 1) × sumă pentru k de 0 la N_L − 1 de (P_{i−k} − m_L(i))² ]
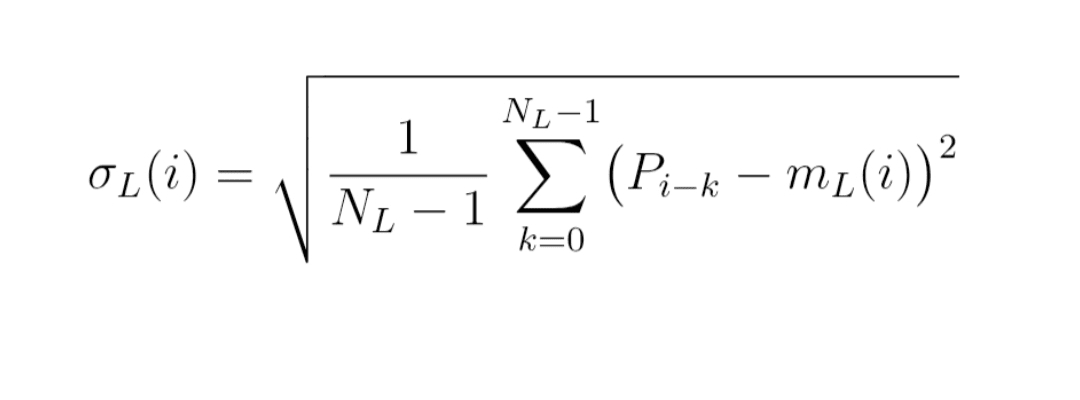
Este pur și simplu deviația standard clasică, calculată pe fereastra glisantă a ultimelor prețuri.
2.2. Benzile de Bollinger
Benzile Bollinger la deviații standard (de obicei k = 2) sunt:
Formulă (3) : benzi
Banda superioară : B_L^înalt(i) = m_L(i) + k × σ_L(i)
Banda inferioară : B_L^jos(i) = m_L(i) − k × σ_L(i)
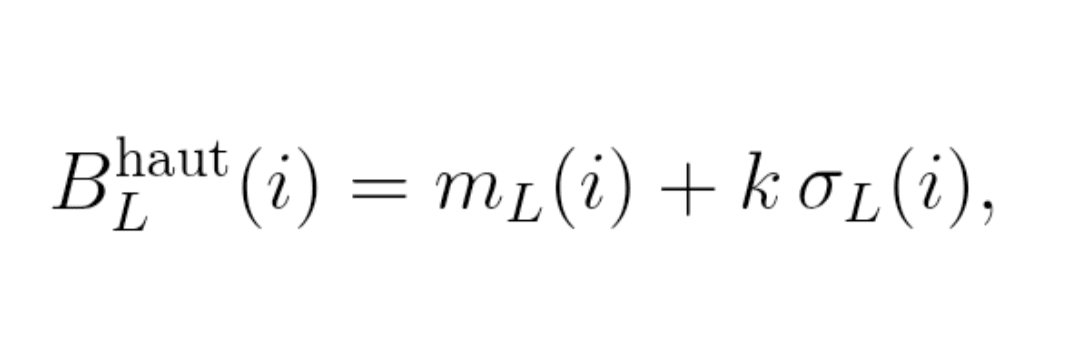
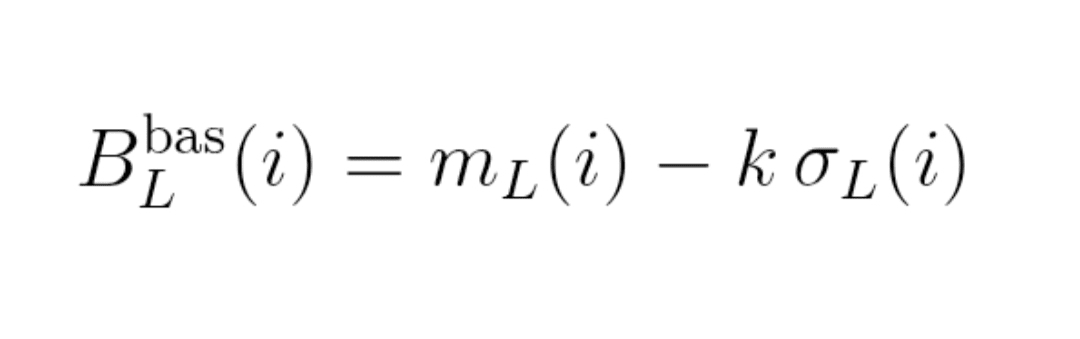
2.3. Preț normalizat în tunel
Apoi ne uităm unde se află prețul în numărul de sigmas:
Formulă (4) : preț normalizat
z_L(i) = (P_i − m_L(i)) / σ_L(i)
z_L(i) ≈ 0 : prețul în centrul tunelului,
|z_L(i)| ≈ 1, 2, 3 : preț care se apropie sau lovește benzile.
Tot ce urmează se desfășoară în acest sistem normalizat z_L.
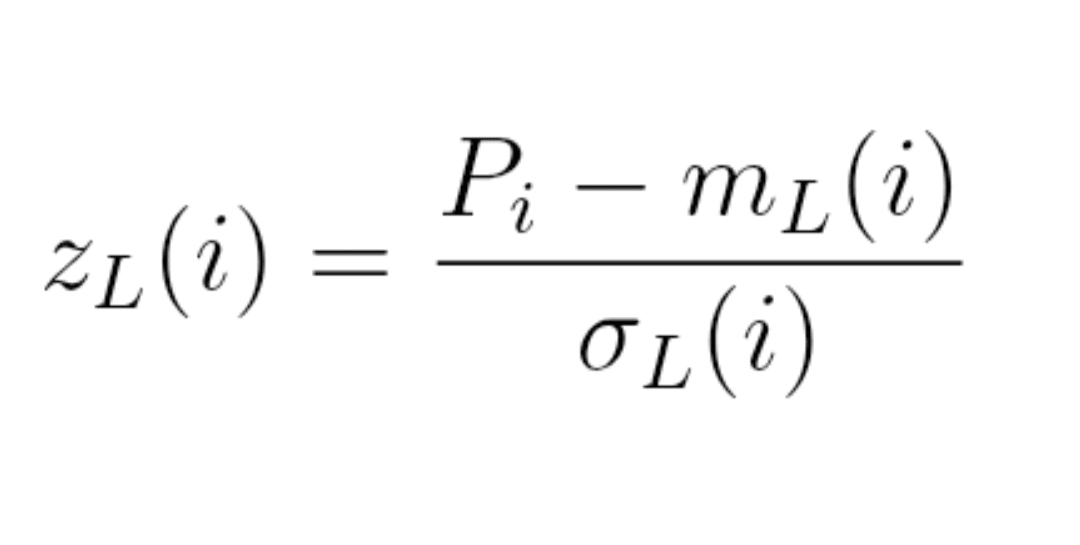
3. Măsoară „rugozitatea” prețului între benzi
Intuiție:
Piață profundă → prețul alunecă mai degrabă lin în tunelul său.
Piață goală → prețul este nervos, neclar, sare foarte repede dintr-o parte în alta a tunelului.
Măsurăm această rugozitate cu o energie de Dirichlet discretă.
Ne plasăm pe o fereastră de indici de la i_0 la i_1.
Formulă (5) : energie E_L
E_L(i_0, i_1)
= 1/2 × sumă pentru i de i_0 la i_1 − 1 de [ z_L(i+1) − z_L(i) ]²
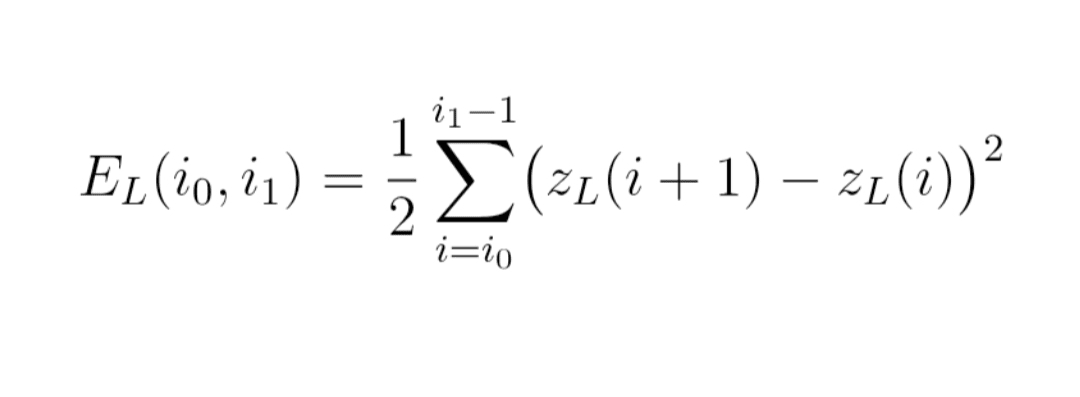
Apoi normalizăm prin lungimea feronței pentru a obține o densitate:
Formulă (6) : densitate de energie ε_L
ε_L(i_0, i_1) = E_L(i_0, i_1) / (i_1 − i_0)
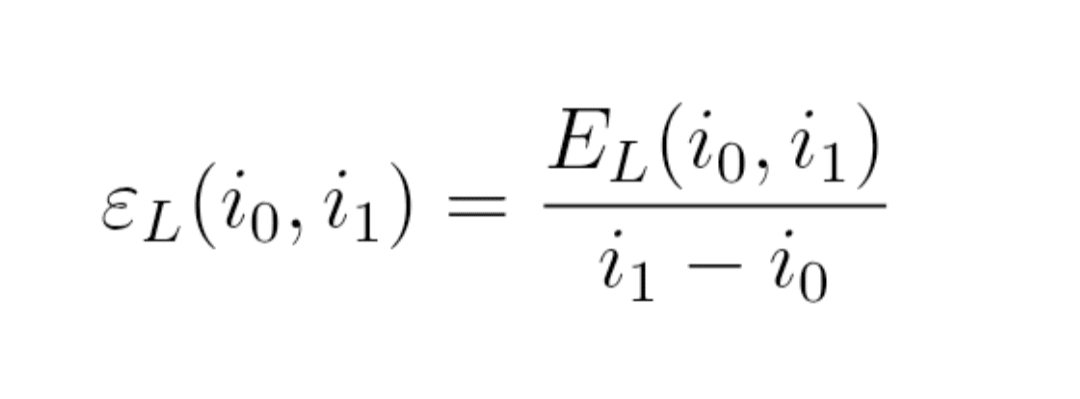
Lectură:
ε_L mic → traiectorie z_L destul de lină,
ε_L mare → traiectorie z_L foarte neclară.
În esență, ε_L măsoară cât de mult prețul „fluctuează” în interiorul tunelului său Bollinger, independent de scala de preț (grație normalizării prin σ_L).
4. Profunzime implicită : un scor simplu Λ_L
Acum dorim să legăm această rugozitate de profunzimea pieței.
4.1. Mic model stilizat
Se notează:
Formulă (7) : randament elementar
r_i = log(P_{i+1}) − log(P_i)
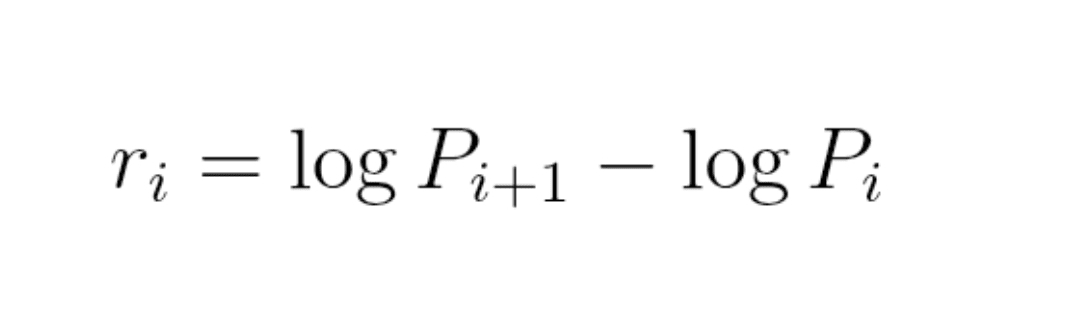
Se presupune un model foarte simplu:
Formulă (8) : model microstructural
r_i = (1 / Λ_i) × q_i + η_i
unde:
q_i = dezechilibru de ordine (buy-uri de piață − sell-uri de piață) pe interval,
Λ_i = profunzimea locală a pieței,
η_i = „zgomot” (știri, flux fundamental...).
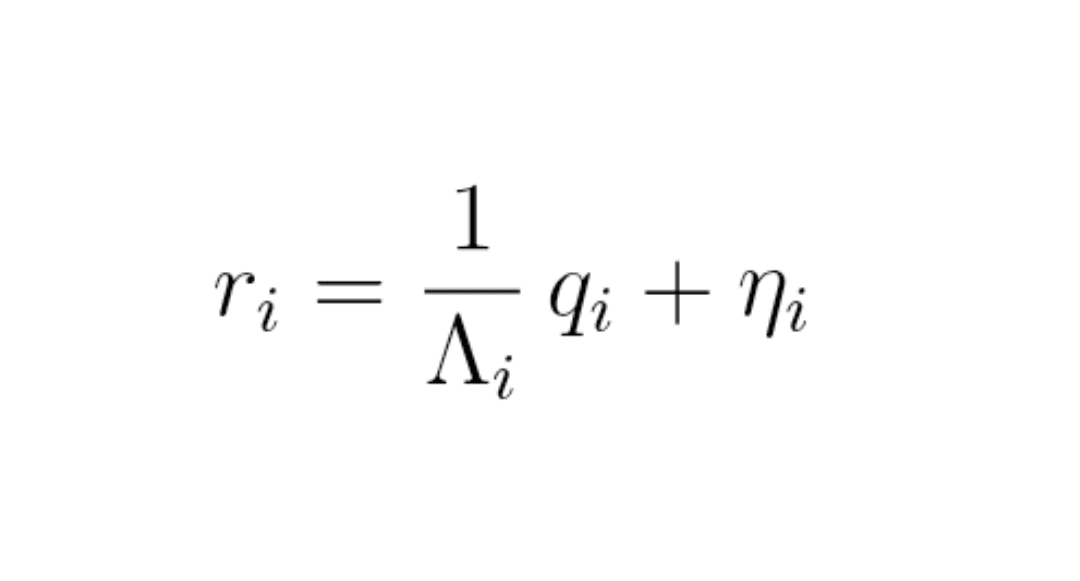
Fără DOM, nu vezi nici q_i nici Λ_i.
Dar vedem r_i, deci z_L, deci ε_L.
Raționând în jurul variațiilor și grupând constantele, ajungem la o relație de tip:
Formulă (9) : variația randamentelor (schema)
E[r_i²] ≈ σ_q² / Λ² + σ_η²
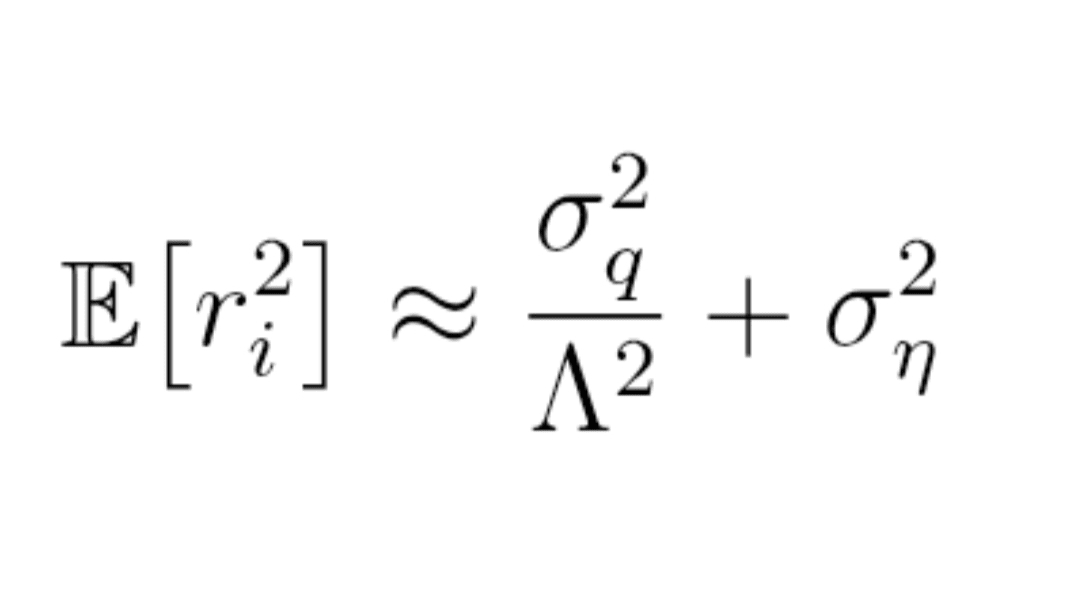
(în medie pe fereastră, σ_q și σ_η sunt constante, Λ profunzimea tipică).
Ideea cheie: cu cât Λ este mai mic, cu atât termenul σ_q² / Λ² este mai mare, deci cu atât r_i² este mai mare → cu atât prețul este mai afectat pentru un flux de ordine similar.
Legând z_L și r_i (z_L este grosso modo randamentul împărțit la σ_L), obținem că ε_L crește când Λ scade.
De unde un scor de profunzime implicit foarte simplu 👇
4.2. Definiție practică a scorului Λ_L
Formulă (10) : scor de profunzime implicit
Λ_L ≈ C_L × σ_L / rădăcină pătrată de ε_L
unde :
σ_L = volatilitate locală,
ε_L = densitate de energie,
C_L = constantă de calibrat pe o pereche unde DOM este vizibil.
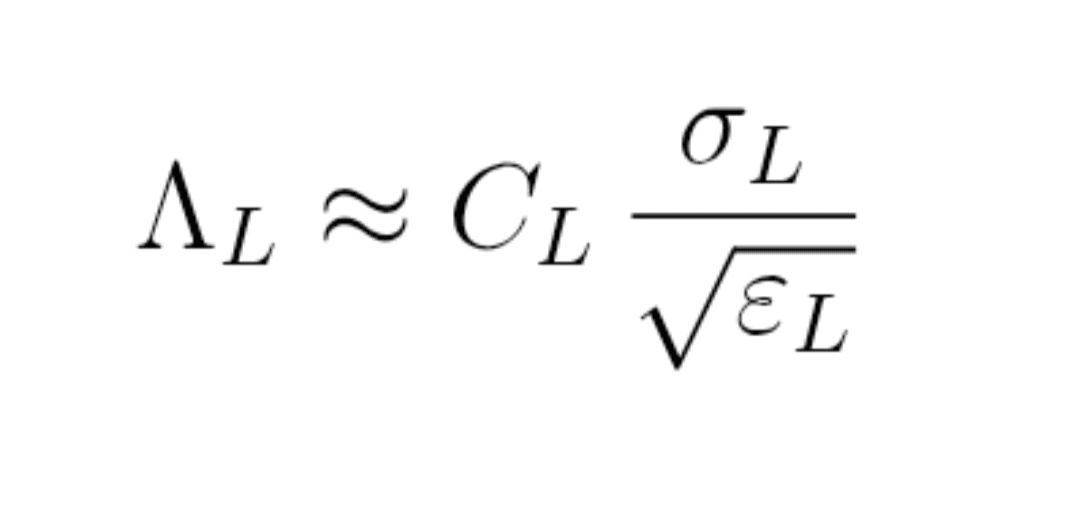
Lectură:
Λ_L mare → piața absoarbe bine fluxurile de ordine → profunzime mare.
Λ_L mic → prețul „scutură” mult pentru același σ_L → piață goală.
Ai acum un indice de profunzime implicit fără a vedea carnetul. 🤩
5. Volum implicit până la benzile
În multe modele de microstructură, volumul necesar pentru a muta prețul cu un anumit Δp este proporțional cu Λ_L × |Δp|.
Dacă ne uităm la ce se întâmplă până la benzile cu k deviații standard:
Δp = k × σ_L.
Atunci putem defini un volum implicit până la benzile:
Formulă (11) : volum implicit V_L^imp
V_L^imp (Δp = k σ_L)
≈ k × C_L × σ_L² / rădăcină pătrată de ε_L
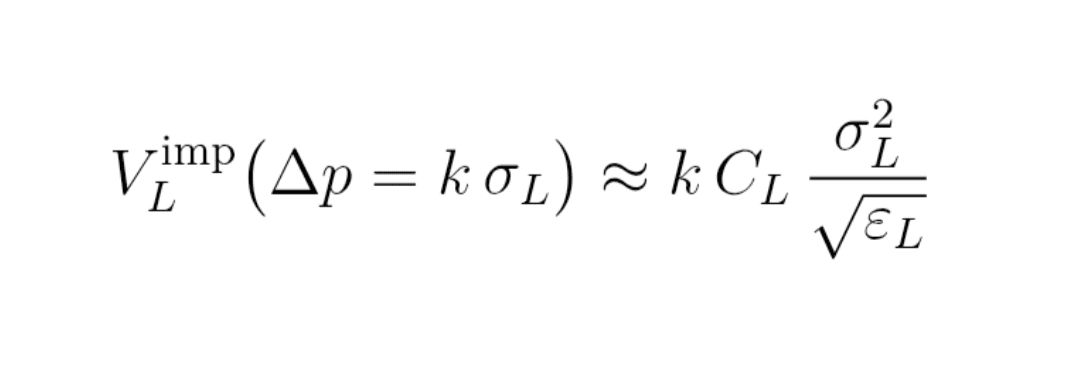
Acest V_L^imp este un ordin de mărime al volumului pe care ar trebui să-l (în medie) pentru a curăța carnetul ascuns până la benzile Bollinger.
Pe o pereche cu DOM, poți compara:
V_L^imp ↔ volum real cumulativ în carnet.
Pe piața Alpha, ai doar V_L^imp… dar este deja o busolă. 🧭
6. Cum să aplici asta pe Binance
6.1. Faza 1 : calibrare pe o pereche cu DOM vizibil
1. Alege o pereche foarte lichidă (BTCUSDT, ETHUSDT Spot).
2. În direct:
recuperează prețurile (tranzacții sau lumânări de 1s),
recuperați instantanee DOM (profundimea cumulată până la ±0,1 %, ±0,5 %, ±1 %, etc.).
3. Pentru fiecare fereastră:
calculează m_L, σ_L, ε_L,
calculează indicatorul brut S_L = σ_L² / rădăcină pătrată de ε_L,
măsoară volumul real V_obs cumulativ în DOM până la Δp = k σ_L.
4. Fă o regresie simplă:
Formulă (12) : relație empirică
V_obs ≈ C_L × S_L
(cu S_L = σ_L² / √ε_L)
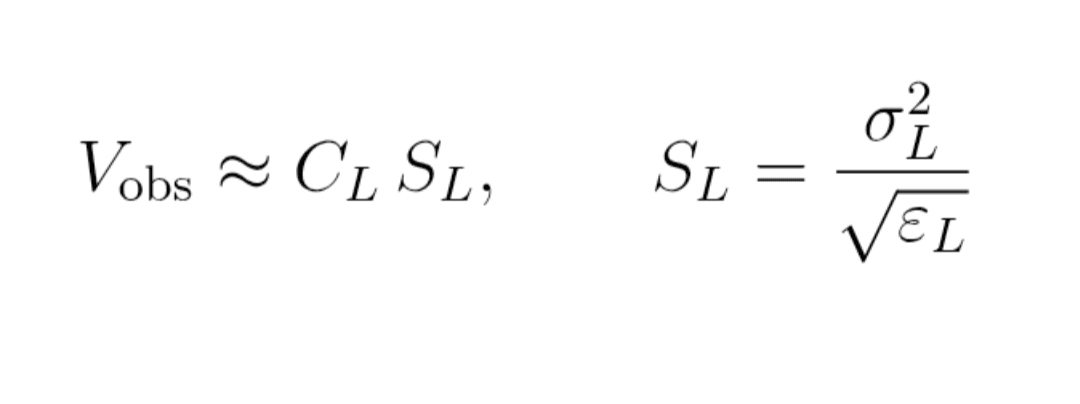
Îți deduci constanta C_L pentru această scală L.
6.2. Faza 2 : aplicație pe piața Alpha (fără DOM)
1. Pe perechea ta Alpha:
recuperează prețurile în direct,
calculează m_L, σ_L, ε_L.
2. Aplică formula:
Formulă (13) : volum implicit final
V_L^imp (Δp = k σ_L) ≈ k × C_L × σ_L² / √ε_L
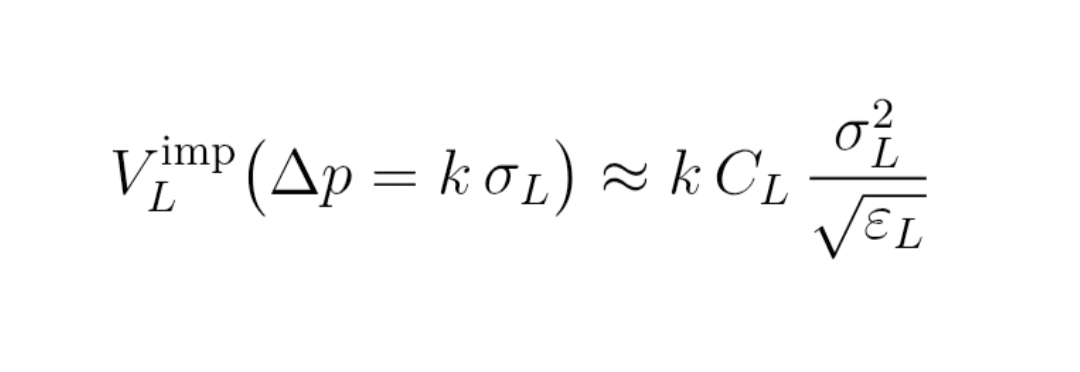
3. Afișează în timp real:
scorul Λ_L,
curba Δp ↦ V_L^imp (DOM-ul tău fantomă).
7. Utilizare concretă pentru ordinele tale
7.1. Construiește un ladder dependent de Λ_L
Dacă Λ_L este mare: piață profundă,
poți:
aproapează nivelurile progresiei tale geometrice,
păstrează dimensiuni ale ordinelor destul de regulate.
Dacă Λ_L este mic: piață goală,
poți:
spacificați mai mult nivelurile,
reduce dimensiunea ordinelor aproape de preț,
păstrează volum pentru nivele mai îndepărtate.
7.2. Citește „găurile de lichiditate” implicite
Privind Λ_L în timp real:
Λ_L scade brusc în timp ce σ_L nu se schimbă mult:
alertă : piața devine fragilă,
poți reduce levierul, lărgi stopurile, evita „piața” prea agresivă.
Λ_L crește după un șoc:
semn de reziliență : profunzimea revine, piața se reîntregește.
8. Limite și bun simț
Nu este un oracle:
nu vede spoofers,
nu înțelege știrile macro,
nu înlocuiește managementul tău de bani.
Indicatorul depinde:
alegerii feronței N_L,
de calitatea calibrării C_L,
din granularitatea datelor.
A se folosi ca:
un radar de profunditate implicită, în complementul analizei tale tehnice,
nu ca un buton magic „buy/sell”.
9. Pentru a merge mai departe
Acest articol oferă versiunea „trader”.
Din spate, există o mică teorie:
funcția z_L văzută ca funcție pe un lanț (graf),
energie de Dirichlet,
legătură cu ecuația căldurii și netezirea progresivă.
Într-un articol matematic separat, vom putea detalia toate acestea în mod corespunzător, cu demonstrații la suport pe contul TikTok @Maths4Traders 💪🤩